Raconter une histoire nous donne un cadre pour certaines tâches mathématiques qui est à la fois assez prescriptif pour être utile et suffisamment flexible pour être utilisable. Plusieurs de ces histoires se divisent en trois actes, chacun d'eux collant parfaitement à ces tâches mathématiques.
Acte 1
Présenter le conflit central de votre histoire/tâche clairement, visuellement, viscéralement, en utilisant le peu de mots possible.
Avec Jaws, votre premier acte ressemblera à ceci:

Le visuel est clair. La caméra est au focus. Elle ne sautille pas pour que vous puissiez garder votre attention sur la scène. Il n'y a pas de mots. Et c'est viscéral. Vous vivez un stress et vous commencez à avoir peur.
En mathématique, votre premier acte ressemblera à ceci:

Le visuel est clair. La caméra est verrouillée sur un trépied et cible la scène. Aucun mot n'est nécessaire. On ne dit pas que l'on paierait pour résoudre ce problème mathématique, mais vous avez une réaction viscérale à l'image. Elle pique votre curiosité.
Ne laissez personne de côté pour votre premier acte. Votre premier acte ne devrait demander que le minimum des élèves au niveau du langage et des mathématiques . Il devrait demander peu et offrir beaucoup.
Acte 2
Le protagoniste/élève surmonte des obstacles, cherche des ressources et développe des nouveaux outils.
Avant qu'il résolve son plus grand conflit, Luke Skywalker en résout plusieurs plus petits: trouver un vaisseau, trouver la princesse, trouver les plans de l'Étoile Noire pour les rapporter à la Rébellion, etc. Il forme une équipe. Il développe de nouvelles habiletés.

Tel est le cas pour votre deuxième acte. Quels ressources vos élèves auront-ils besoin pour résoudre leur conflit ? La hauteur du panier de basketball ? La distance jusqu'à la ligne de 3 points ? Le diamètre du ballon ?
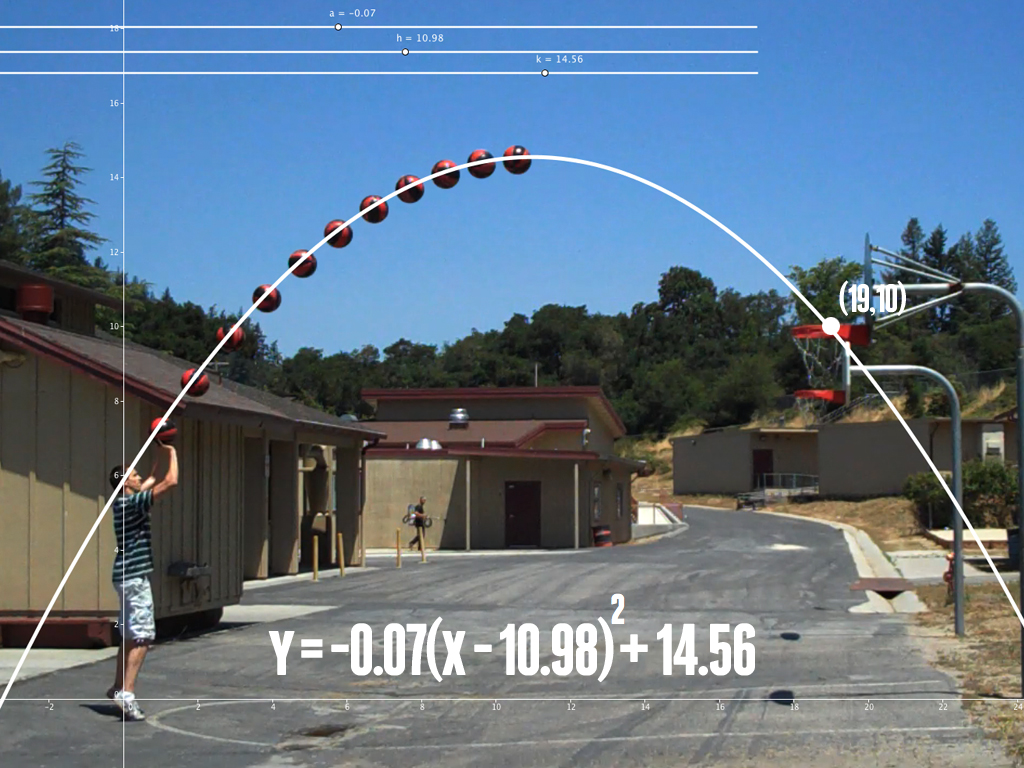
Quels outils ont-ils déjà ? Quels outils pouvez-vous les aider à développer ? Par exemple, ils auront besoin de la fonction quadratique. Aidez-les avec ceci.
Acte 3
Résoudre le conflit et mettre en place une suite/extension.
Le troisième acte est payant et est en lien avec le travail effectué au deuxième acte et la motivation de l'élève lors du premier acte. Voici le troisième acte de Star Wars.

Voici une belle résolution. Imaginez lorsque Luke tire son dernier coup, au lieu de voir l'Étoile Noire exploser, la scène nous transporte dans la salle des commandes de la Rébellion. Pas d'explosion. Seulement le commandant qui nous annonce que la mission a été un succès.
C'est ce qui arrive aux élèves qui résolve leur conflit en trouvant la réponse à la fin du manuel.
"Le ballon va entrer dans le panier".
Si nous avons motivé nos élèves suffisamment dans le premier acte,il faut que ce soit une paie satisfaisante dans le troisième acte. Un peu comme ceci:

Souvenez-vous de Darth Vader qui s'enfonce dans l'espace, qui jette les bases pour le deuxième film, l'Empire contre-attaque. Vous devez être Vader. Assurez-vous que vous avez des problèmes pour assurer le suivi lorsque les élèves ont terminé.
Conclusion
Plusieurs enseignants prennent le deuxième acte comme leur définition de tâche. Offrez trois exemples détaillés au tableau avec vingt exemples que les élèves doivent faire. Il est clair que le deuxième acte n'est plus notre travail. Du moins, pas la majeure partie. Vous êtes l'une de plusieurs personnes que les élèves peuvent consulter lorsqu'ils recherchent ressources et outils.
Dorénavant, la valeur que vous apportez à votre classe de mathématiques sera payante dans le premier et troisième acte, votre capacité à motiver dans le deuxième acte et ensuite sera payant sur le travail effectué par les élèves.
(Traduction libre du blogue de Dan Meyer, que vous retrouverez ici: http://blog.mrmeyer.com/?p=10285)





